Wat is de kans? – Dertigen

Door Jos Zuijderwijk (gastartikel)

Voor de student is er één drankje essentiëler dan koffie: bier. Waar koffie zich matig leent voor een spelelement, zijn drankspellen op basis van bier schering en inslag in de studentencultuur. Niet zonder reden: een drankspel is niet zomaar een spel waarbij er louter stevig gedronken wordt – neen! Cruciaal is een mooie balans tussen kans en strategie. Immers zouden anders alle spelletjes te reduceren zijn naar ‘kop of munt voor een bak’ – overigens wel een stuk efficiënter.

Hoewel dit type spel per definitie alleen maar winnaars kent, is het interessant om na te denken hoe je het slimst kunt spelen. Een strategie kun je maar beter van tevoren hebben uitgedacht; als je eenmaal aan het verliezen bent, kan het zijn dat nadenken steeds lastiger wordt. Als je eenmaal een strategie hebt die werkt, kun je spellen met elkaar vergelijken. Welke gaat het hardst?

In deze gastrubriek analyseer ik dit soort spelletjes: hoe hard gaan ze nou echt? Deze keer behandelen we dertigen. Misschien niet het meest populaire spel, maar toch zeker één waarbij je je kansen van tevoren kunt inschatten. Laten we beginnen met een korte uitleg van de regels. Het is altijd taai om een speluitleg aan te horen, laat staan te lezen, daarom zal ik het beknopt houden. Toch loont het om de speluitleg te lezen! Aan het einde heb je namelijk een nieuw spel geleerd wat op zichzelf vet leuk is.

Regels

Men neme zes dobbelstenen en een biertje naar keuze. Een speler gooit zes dobbelstenen tegelijkertijd. Na iedere worp moet de speler dobbels ‘sparen’. Deze dobbels worden dan aan de kant gelegd en tellen mee in het uiteindelijke aantal punten van die beurt. Overige dobbels worden opnieuw gegooid. Je moet alle dobbels met dezelfde waarde pakken; je mag dus niet één van de twee geworpen zessen sparen en de andere niet.

Voorbeeld 1. De speler gooit (1,3,3,6,6,6). Dan mag de speler (1), (3,3) óf (6,6,6) pakken. De overige dobbels moeten dan opnieuw geworpen.

Het doel van het spel is om de som van alle gespaarde dobbels bóven de dertig uit te laten komen. In voorbeeld 1 is het dus het verstandigste om de zessen te sparen en (1,3,3) opnieuw te gooien. De speler blijft gooien en sparen tot er geen dobbels meer over zijn om te gooien. Er zijn dus maximaal zes worpen per speler.

Voorbeeld 2. Een beurt kan er dus als volgt uit zien. Gooi (1,3,3,6,6,6). Spaar (6,6,6). Gooi (3,5,5). Spaar (5,5). Gooi (3). Spaar (3). Score = 6+6+6+5+5+3 = 31.

Daarna is de volgende speler aan de beurt totdat iedereen geweest is.

Score

Je score na een beurt is dus gelijk aan het aantal gespaarde ogen. Maar wat doen we ermee? Laten we de score even $s$ noemen.

• Als $s < 30$, drink je tweemaal het verschil aan slokken: $ 2 \cdot (30-s$).
• Als $s = 30$ is dat saai. Je drinkt zelf een halve bak.
• Als $s > 30$ winst! Je hebt gewonnen. Je mag slokken uitdelen gelijk aan $s-30$ én verdergaan met sparen.

Laten we even ingaan op de laatste variant: winst.

Voorbeeld 3. Een speler eindigt met 34. Dan mag hij sowieso vier slokken uitdelen en verder ‘voor de vieren’ gooien. De speler begint dan weer met zes dobbelstenen en mag alleen de vieren sparen. De rest wordt opnieuw gegooid. Als er geen vieren zijn mag je niet meer opnieuw gooien. Stel dat je drie vieren weet te sparen, mag je 4 + (3*4) = 16 slokken uitdelen.

Speciale regels

Als je tot hier gekomen bent, zul je vast ook wel geïnteresseerd zijn in de speciale regels. De belangrijkste is duiken. Duiken houdt in dat je een score probeert te gooien onder de tien. In principe mag je altijd duiken, maar als je in je eerste worp meer enen dan zessen gooit, moet je duiken. Als je er eenmaal voor kiest om te duiken, moet je de dobbels pakken die het nog mogelijk maken om een score onder de tien te krijgen. Bijkomend voordeel is dat als je het niet redt, je niet het dubbele verschil met 30 hoeft te drinken, maar slechts het verschil. Als je het wel redt, trekt iedere andere speler een halve bak.

• Als $s < 10$ winst! Iedere andere speler trekt een halve bak.
• Als $10 < s < 30$, drink je het verschil: $30 – s$ slokken.

Voorbeeld 4. Een speler gooit (1,3,3,4,5,5). Hij moet dus duiken en spaart (1). Hij gooit (2,2,4,5,5). Met (2,2) kan $s<10$ nog gehaald worden, dus spaar (2,2). Hij gooit (3,3,5). Nu kan het niet meer gehaald worden. Spaar (5). Gooi (6,6). Spaar (6,6). Score = 1 + 2 + 2 +5 + 6 + 6 = 22. Drink $30 – s = 8$ slokken.

Verder heb je nog een tweetal speciale gevallen. Als je in één keer een regenboog (of grote straat) werpt (1,2,3,4,5,6) heb je direct gewonnen en trekt iedere andere speler een halve bak. Als je in één keer zes dezelfde dobbels gooit, bijv. (1,1,1,1,1,1), mag je gelijk voor dat aantal gaan sparen (in dit geval alsof je wint met 31).

Kans

Dan nu de hoofdvraag: hoe zit het met je kansen in dit spel? Dat kunnen we uitzoeken met statistiek. Zo is de gevleugelde uitspraak “je kunt niet altijd zes gooien” toch zeker in $100\%$ van de gevallen waar. Je kunt in je eerste worp maar liefst $6^6 =46656$ verschillende mogelijkheden gooien: te veel om tijdens een spelletje allemaal door te rekenen. Laten we eerst kijken naar onze speciale regels.

• Er zijn verschillende manieren om een regenboog (1,2,3,4,5,6) te gooien: namelijk alle permutaties, volgordes, van die getallen. Dan is de kans op $P(X = regenboog) = \dfrac{6!}{6^6} \approx 1.5\%$. Dat valt mee!
• De kans op zesmaal dezelfde dobbel is aanzienlijk kleiner. Er zijn namelijk maar zes opties. Dus $P(X = (x,x,x,x,x,x)) = \dfrac{6}{6^6} \approx 0.013\%$

Oké, maar hoe groot is de kans dan dat je een score van hoger dan 30 haalt? Tsja. Dat kún je uitrekenen met klassieke kansberekening, maar dat is best pittig. Je moet dan namelijk rekening houden met heel veel mogelijkheden. Het moeilijke zit in het feit dat een speler iedere ronde meerdere keren moet sparen. De kans dat je eindigt met zes zessen is bijvoorbeeld veel groter dan dat je die in één keer gooit, daarvoor zou je de kansen dat je zes in $1 < i < 6$ keer gooit bij elkaar moeten optellen. De kans dat je wint, vind je dan door dat voor alle permutaties zodanig dat $s > 30$. In plaats daarvan is het veel eenvoudiger om te kijken naar een computersimulatie. Krijg je ook van die kekke plotjes van.

Strategie

Om te beginnen met een simulatie, moeten we eerst de strategie van de speler bepalen. We bekijken een eenvoudige strategie die (in mijn ervaring) het meeste voorkomt, namelijk: pak altijd de hoogste dobbels. Maar werkt dit altijd? Er zijn af en toe van die twijfelgevallen. Kun je soms niet beter settelen voor meerdere lagere dobbels?

Voorbeeld 5. Een speler heeft al drie dobbelstenen gespaard. Hij gooit vervolgens (5,5,6).

In het voorbeeld pakt de speler die onze strategie volgt de dobbel met de hoogste ogen: 6. Dan gooit hij (5,5) opnieuw. Er zijn 36 mogelijkheden, waarvan 6 de beurt direct beëindigen (dubbele getallen). In de overige 30 gevallen werpt de speler de kleinste dobbel opnieuw. De verwachtingswaarde van één dobbel $E(X = \text{1 dobbel}) = 3.5$. Voor zes sparen krijgen we dan de volgende draak van een verwachtingswaarde (met drie stenen):

\begin{align*}\mathbb{E}(X = \text{gooi 2 vijven} ) &= 6 + \prod_{i=1}^{k=6}{\dfrac{1}{36} (2i)} \\&+ \sum_{i = 1}^{k=5}{\frac{2i}{36} \cdot ((i+1) \\ + \mathbb{E}(X = \text{1 dobbel}))} \\ &= 13.972\end{align*}

Dan nu de alternatieve strategie! Als de speler (5,5) houdt en 6 opnieuw gooit dan:

$$\mathbb{E}(X = \text{spaar } (5,5)) = 10 + \mathbb{E}(X = \text{1 dobbel}) = 13.5$$

Het loont dus om 6 te pakken (omdat je dan naar verwachting hoger eindigt). Maar geldt dat nog steeds als we het aantal vijven opschroeven? (Dit keer uitgerekend met een scriptje)

$k$	$\mathbb{E}(\text{gooi } k \text{ vijven})$	$\mathbb{E}(\text{spaar } k \text{ vijven})$
2	13,972	13,5
3	18,944	18,5
4	24,202	23,5
5	29,65	28,5

Nou blijkbaar wel. Het lijkt erop dat deze strategie redelijk werkt. Daarmee is het nog niet bewezen dat-ie ook optimaal is, daarvoor zouden we andere situaties moeten bekijken, zoals: kies je (2,2,2,2,2) of (1) ? Mijn vermoeden is dat er ergens een kantelpunt bestaat waarbij het aantrekkelijker is om de lagere dobbel te pakken.

Wat doen we qua strategie met duiken? Dat is al aardig vastgelegd door de regels, namelijk: duik als je meer enen dan zessen in je eerste worp gooit. Zolang je nog een som onder de tien kan halen: pak de laagste dobbel. Anders: pak de hoogste dobbel.

Simulatie van een beurt

Nu we een strategie hebben, kunnen we die de computer supervaak laten uitvoeren. We modelleren slokken zelf nemen als negatieve slokken. Een hele bak stellen we gelijk aan 15 slokken (halve bak ronden we naar boven af, dus 8 slokken). In deze eerste simulatie kijken we naar één beurt (dus van één speler). Hierbij is duiken nog niet meegerekend. Een run van 10.000 keer levert de volgende resultaten op.

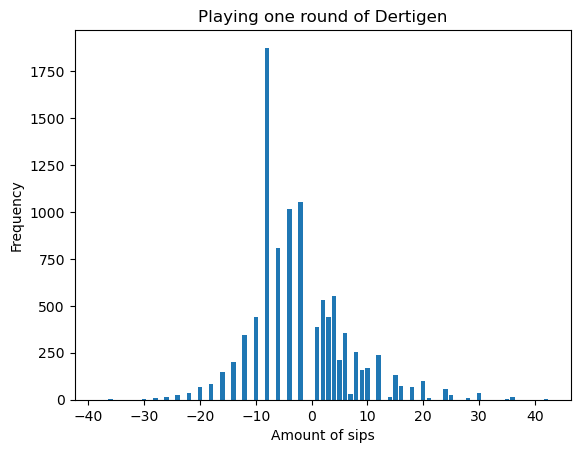
We zien een piek op -8. Dat moet die halve bak zijn die je krijgt als je precies 30 (saai) gooit! We kunnen ook de volgende waarden benaderen:

• De kans dat je wint (dus mag uitdelen) is 37,97%;
• Het gemiddeld aantal slokken dat je mag uitdelen als je wint is 7,09;
• De mediaan van het aantal uit te delen slokken is 5;
• De kans dat je verliest is 62,03%;
• Het gemiddeld aantal slokken dat je zelf moet nemen is 7,32;
• De mediaan van het aantal te nemen slokken is 8.

De mediaan is hierbij wellicht een intuïtievere maat dan het gemiddelde, omdat we hier geen normale verdeling hebben. Afijn, best grote kans om je eigen ronde goed uit te spelen dus! Wat gebeurt er als we duiken toevoegen?

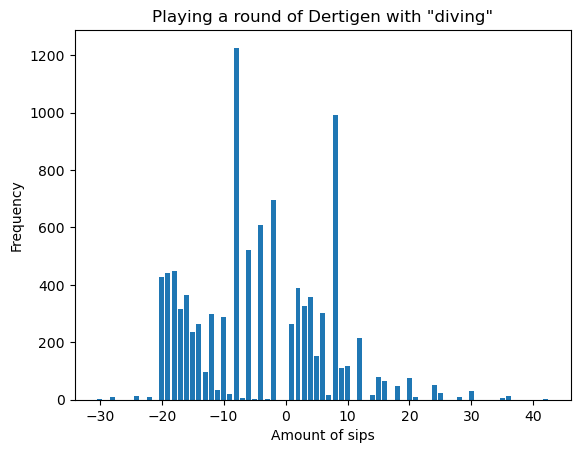
Aha! Een interessante verdeling. Nu hebben we twee pieken! Dit zijn wederom halve bakken: de kleinere is voor de geslaagde duikers (die mag een halve bak uitdelen). Laten we kijken hoe groot de kans is dat je als duiker wint.

• De kans dat je moet duiken is 33,49%;
• De kans dat je wint als duiker is 24,22%;
• Dus de kans dat er een winnende duiker is, is 8,11%.

En wat doet dit met onze winkansen?

• De kans dat je wint is 37,09%;
• Het gemiddeld aantal slokken dat je mag uitdelen als je wint is 7,56;
• De mediaan van het aantal uit te delen slokken is 8;
• De kans dat je verliest is 62,91%;
• Het gemiddeld aantal slokken dat je zelf moet nemen is 11,0;
• De mediaan van het aantal te nemen slokken is 9.

Het (naar boven afgeronde) verwachte aantal zelf te drinken slokken van een spel zonder duiken is 5, en met duiken 7. Het wordt dus iets grimmiger t.o.v. de situatie zonder duikers. Maar dat hou je toch.

Is dit alles? Kunnen we al conclusies trekken? Daar is het nog iets te vroeg voor. Meestal speel je dit namelijk niet in je eentje (hopelijk). Wat gebeurt er als je een rondje speelt met meerdere spelers?

Simulatie van een spelronde

We spelen het spel 100.000 keer met vier spelers. Jíj begint iedere keer. Dan volgen de drie resterende spelers. Je drinkt uiteraard de slokken die je zelf moet drinken. De slokken die worden uitgedeeld door je medespelers worden uniform verdeeld (is ook wat voor te zeggen, als je uitgaat van solidaire regels). De halve bakken (bijvoorbeeld als je medespeler wint met duiken) krijg je natuurlijk wel als geheel en worden niet verdeeld. Laten we kijken wat dit doet met het aantal slokken.

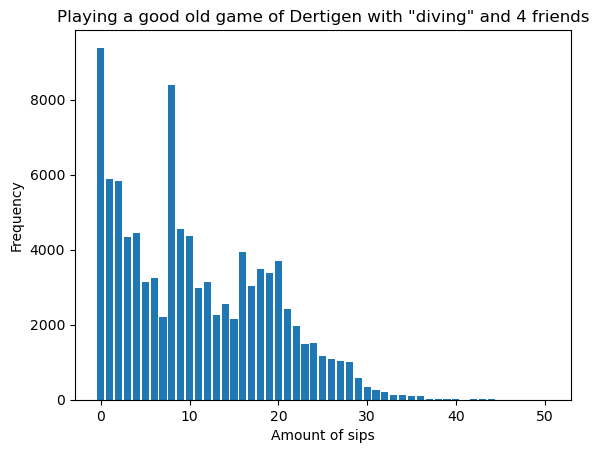
Het gemiddelde aantal slokken is nu 11 voor een heel spel. De mediaan is 9.

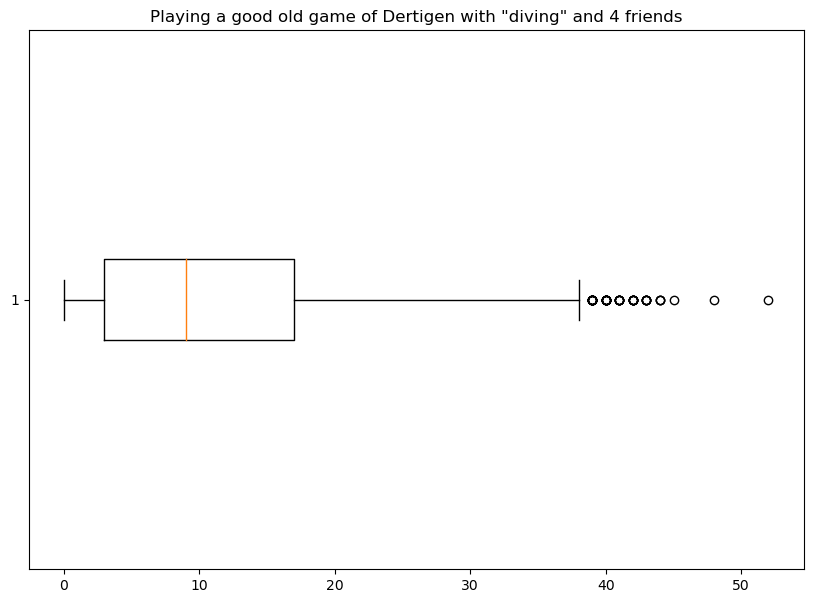
De notebook (of PDF) van de simulatie zijn beschikbaar via de links.

Conclusie

Om echt uit te zoeken hoe hard het gaat zou je moeten kijken naar het aantal slokken over de tijd: de slokdichtheid van het spel. Als we uitgaan dat een spelletje met vier personen ongeveer acht minuten duurt (twee minuten p.p.) dan hebben we het over gemiddeld 1,38 slokken per minuut.

Er zijn natuurlijk nog talloze andere spellen, denk aan bussen, mexxen, klaverboeren (favorietje), ‘boer-zoekt-vrouw’ of het op Orca steeds populairdere ‘vierkantje leggen’. Benieuwd of die ook hard gaan? Of heb je misschien zelf een spel dat je altijd al wilde ontrafelen? Stuur dan een mailtje naar de Blikredaxi. Bij genoeg animo schud ik nog een analyse uit mijn spreekwoordelijke mouw. Mocht je een foutje hebben ontdekt, laat het dan ook vooral weten!

#	Spel	Slokdichtheid (p/min)	Mediane aantal slokken
1	Dertigen	1,38	9
	????